Introduction to HOIF: Higher Order Influence Function Estimators for ATE

Xingyu Chen

2026-01-30

Introduction

The HOIF package implements Higher Order Influence Function (HOIF) estimators for Average Treatment Effect (ATE) estimation in causal inference. This methodology extends the doubly robust (DR) estimator—also known as the Augmented Inverse Propensity Weighted (AIPW) or Double Machine Learning (DML) estimator—by systematically accounting for higher-order bias terms.

Background

The HOIF methodology was developed through a series of seminal works by James M. Robins and collaborators:

• Robins et al. (2008): Higher order influence functions and minimax estimation of nonlinear functionals
• Robins et al. (2017): Minimax estimation of a functional on a structured high-dimensional model
• Liu et al. (2017): Semiparametric regression in the presence of control variables
• Liu & Li (2023): Stable higher order influence function estimation

The key idea is to represent the bias of the standard DR estimator as a sum of higher-order influence functions, which can be estimated and used to debias the original estimator.

Key Features

• Flexible basis expansion: Supports B-splines, Fourier basis, or raw covariates
• Multiple inversion methods: Direct, nonlinear shrinkage, or corpcor regularization
• Sample splitting support: Optional K-fold cross-fitting to avoid overfitting
• Dual computational backends: Fast Python implementation via ustats package or pure R fallback
• Orders 2-7: Computes HOIF estimators up to 7th order (6th order in pure R mode)

Installation

# Install from GitHub (example)
# devtools::install_github("yourusername/HOIF")

# Or from CRAN (if published)
# install.packages("HOIF")

Quick Start Example

Let’s demonstrate the basic usage with a simple simulated example.

Generate Simulated Data

set.seed(123)
n <- 500
p <- 2

# Generate covariates
X <- matrix(rnorm(n * p), ncol = p)

# True propensity score
true_pi <- plogis(0.5 * X[,1] - 0.3 * X[,2])

# Generate treatment
A <- rbinom(n, 1, true_pi)

# True outcome functions
mu1_true <- 1 + 0.5 * X[,1] + 0.3 * X[,2]^2
mu0_true <- 0.3 * X[,1] - 0.2 * X[,2]

# Generate outcomes
Y <- A * mu1_true + (1 - A) * mu0_true + rnorm(n, 0, 0.5)

# True ATE
true_ate <- mean(mu1_true - mu0_true)
cat("True ATE:", round(true_ate, 4), "\n")
#> True ATE: 1.3124

Estimate Nuisance Functions

In practice, these would be estimated using machine learning methods on a separate sample.

# For this example, we'll use simple linear models
# (In practice, use cross-fitting with flexible ML methods)

fit_mu1 <- lm(Y ~ X, subset = A == 1)
fit_mu0 <- lm(Y ~ X, subset = A == 0)
fit_pi <- glm(A ~ X, family = binomial)

# Predict nuisance functions
mu1_hat <- predict(fit_mu1, newdata = data.frame(X = X))
mu0_hat <- predict(fit_mu0, newdata = data.frame(X = X))
pi_hat <- predict(fit_pi, type = "response")

# Ensure propensity scores are bounded away from 0 and 1
pi_hat <- pmax(pmin(pi_hat, 0.95), 0.05)

Compute HOIF Estimators

# Compute HOIF estimators without sample splitting
results <- hoif_ate(
  X = X,
  A = A,
  Y = Y,
  mu1 = mu1_hat,
  mu0 = mu0_hat,
  pi = pi_hat,
  transform_method = "none",  # Use raw covariates
  inverse_method = "direct",
  m = 5,                       # Compute up to 5th order
  sample_split = FALSE,
  backend = "torch"            # Use Python backend
)

# View results
print(results)
#> HOIF Estimators for Average Treatment Effect
#> =============================================
#> 
#> Estimates by order:
#>   Order    ATE  HOIF1 HOIF0
#> 1     2 0.0015 0.0016 2e-04
#> 2     3 0.0015 0.0017 2e-04
#> 3     4 0.0015 0.0017 2e-04
#> 4     5 0.0015 0.0016 2e-04
#> 
#> Final ATE estimate (highest order): 0.0015

Visualize Convergence

plot(results)

Main Function: hoif_ate()

The primary interface for computing HOIF estimators.

Arguments

• X: Covariate matrix ($n \times p$)
• A: Treatment vector (0 or 1)
• Y: Outcome vector
• mu1, mu0: Predicted outcomes under treatment and control
• pi: Predicted propensity scores
• transform_method: Covariate transformation method
  • "none": No transformation (use raw covariates)
  • "splines": B-splines basis expansion
  • "fourier": Fourier basis expansion
• basis_dim: Number of basis functions (required if using splines or Fourier)
• inverse_method: Method for Gram matrix inversion
  • "direct": Moore-Penrose pseudoinverse
  • "nlshrink": Nonlinear shrinkage (Ledoit-Wolf)
  • "corpcor": Shrinkage via corpcor package
• m: Maximum order (2-7 for Python backend, 2-6 for pure R)
• sample_split: Logical; whether to use K-fold cross-fitting
• n_folds: Number of folds for sample splitting
• backend: "torch" (default) or "numpy" for Python backend
• pure_R_code: Use pure R implementation (limited to order 6)
• seed: Random seed for reproducibility

Return Value

A list of class "hoif_ate" containing:

• ATE: Vector of ATE estimates for orders 2 to m
• HOIF1: Vector of treatment arm HOIF estimates
• HOIF0: Vector of control arm HOIF estimates
• IIFF1: Vector of treatment arm incremental influence function terms
• IIFF0: Vector of control arm incremental influence function terms
• orders: Vector of orders (2:m)
• convergence_data: Data frame for plotting

Advanced Usage

Using Basis Expansion

For more flexible modeling of covariate relationships:

# B-splines basis
results_splines <- hoif_ate(
  X = X, A = A, Y = Y,
  mu1 = mu1_hat, mu0 = mu0_hat, pi = pi_hat,
  transform_method = "splines",
  basis_dim = 5,        # 5 basis functions per covariate
  degree = 3,           # Cubic splines
  m = 5,
  sample_split = FALSE
)

# Fourier basis
results_fourier <- hoif_ate(
  X = X, A = A, Y = Y,
  mu1 = mu1_hat, mu0 = mu0_hat, pi = pi_hat,
  transform_method = "fourier",
  basis_dim = 4,        # 4 Fourier components per covariate
  period = 1,
  m = 5,
  sample_split = FALSE
)

Sample Splitting (Cross-Fitting)

To avoid overfitting bias when using the same data for both nuisance estimation and HOIF computation:

results_cf <- hoif_ate(
  X = X, A = A, Y = Y,
  mu1 = mu1_hat, mu0 = mu0_hat, pi = pi_hat,
  transform_method = "none",
  m = 5,
  sample_split = TRUE,
  n_folds = 5,          # 5-fold cross-fitting
  seed = 42
)

Regularized Gram Matrix Inversion

For high-dimensional settings or when facing numerical instability:

# Nonlinear shrinkage
results_nlshrink <- hoif_ate(
  X = X, A = A, Y = Y,
  mu1 = mu1_hat, mu0 = mu0_hat, pi = pi_hat,
  inverse_method = "nlshrink",
  m = 5
)

# corpcor shrinkage
results_corpcor <- hoif_ate(
  X = X, A = A, Y = Y,
  mu1 = mu1_hat, mu0 = mu0_hat, pi = pi_hat,
  inverse_method = "corpcor",
  m = 5
)

Pure R Backend

If the Python environment is not available or for smaller problems:

results_pure_r <- hoif_ate(
  X = X, A = A, Y = Y,
  mu1 = mu1_hat, mu0 = mu0_hat, pi = pi_hat,
  pure_R_code = TRUE,
  m = 6  # Maximum 6 for pure R
)

Mathematical Background

The HOIF Framework

The HOIF estimator for ATE is defined as:

$$\mathbb{ATE}_m(\hat{\Omega}^a) = \mathbb{HOIF}^1_m - \mathbb{HOIF}^0_m$$

where for each treatment arm $a \in \{0,1\}$:

$$\mathbb{HOIF}^a_m(\hat{\Omega}^a) = \sum_{j=2}^m \mathbb{IF}^a_j(\hat{\Omega}^a) = \sum_{i=2}^m \sum_{j=2}^{i} \binom{i-2}{i-j} \mathbb{U}^a_j(\hat{\Omega}^a)$$

U-Statistics Formulation

The core computational building block is the U-statistic:

$$\mathbb{U}^a_m(\hat{\Omega}^a) = (-1)^m \frac{(n-m)!}{n!} \sum_{\substack{(i_1, \ldots, i_m) : \\ i_1 \neq \cdots \neq i_m}} r^a_{i_1} \prod_{s=1}^{m-1} \{Z_{i_s}^\top \hat{\Omega}^a s^a_{i_{s+1}} Z_{i_{s+1}}\} R^a_{i_m}$$

where:

• $s^a_i = A_i^a (1-A_i)^{1-a}$ is the treatment indicator
• $r^a_i = 1 - s^a_i / \pi^a(X_i)$ is the inverse propensity weight residual
• $R^a_i = Y_i - \hat{\mu}(a, X_i)$ is the outcome residual
• $Z_i$ are the transformed covariates
• $\hat{\Omega}^a$ is the inverse weighted Gram matrix

Sample Splitting

When using K-fold cross-fitting, for each fold $j$:

1. Training: Use observations not in fold $j$ to compute $\hat{\Omega}^a_j$
2. Estimation: Use observations in fold $j$ with $\hat{\Omega}^a_j$ to compute HOIF
3. Aggregation: Average across all folds

This prevents overfitting and provides valid inference properties.

Computational Details

Python Backend (ustats)

The default backend uses the ustats Python package for efficient U-statistic computation:

• Supports PyTorch and NumPy backends
• Handles arbitrary order U-statistics
• Optimized for memory and speed

Pure R Implementation

The pure R fallback (pure_R_code = TRUE):

• Implements orders 2-6 using recursive matrix operations
• Uses the SMUT package for fast matrix multiplication
• Removes diagonal contributions to ensure proper degenerate U-statistics
• Suitable for smaller datasets or when Python is unavailable

Performance Considerations

• Sample size: Pure R is suitable for $n < 1000$; Python backend scales better
• Order: Higher orders increase computation time exponentially
• Basis dimension: Larger basis increases memory and computation
• Cross-fitting: Multiplies computation by number of folds

Practical Recommendations

Choosing the Transformation Method

• “none”: Start here for low-dimensional problems ($p < 5$)
• “splines”: Good for smooth nonlinear relationships
• “fourier”: Suitable for periodic patterns or high-frequency features

Choosing the Order

• Start with order 3-4 for initial analysis
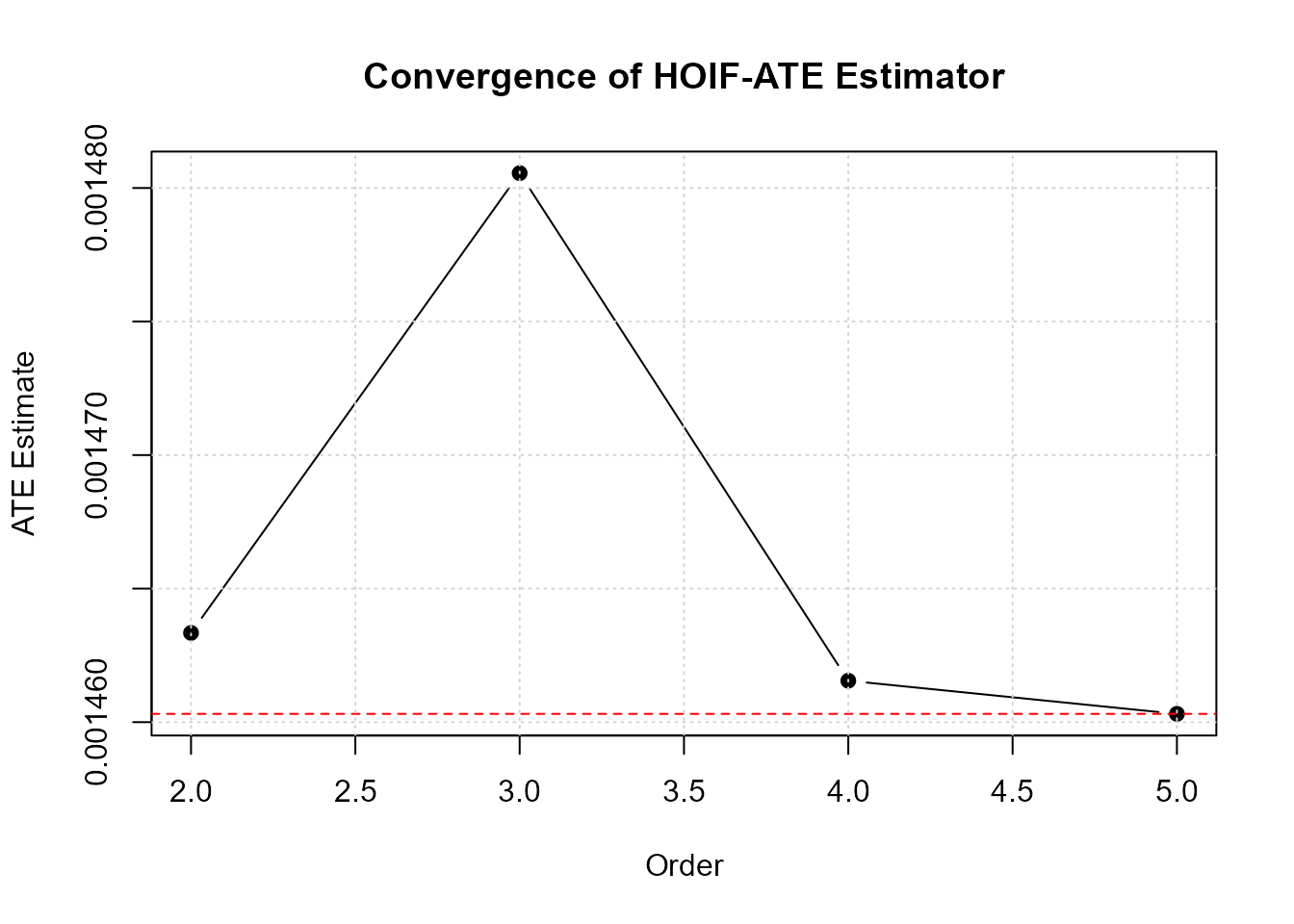
• Check convergence plot to see if higher orders are needed
• Orders beyond 6 rarely improve estimation in practice

Choosing the Inverse Method

• “direct”: Default; works well when $n >> k$ (sample size much larger than basis dimension)
• “nlshrink”: Use when basis dimension is large relative to sample size
• “corpcor”: Alternative shrinkage method, sometimes more stable

Sample Splitting

• Always use when nuisance functions are estimated on the same data
• 2-5 folds typically sufficient
• More folds = less bias but higher variance

Example: Complete Workflow

Here’s a complete example with best practices:

# 1. Load data
data <- read.csv("your_data.csv")
X <- as.matrix(data[, c("age", "income", "education")])
A <- data$treatment
Y <- data$outcome

# 2. Estimate nuisance functions with cross-fitting
library(SuperLearner)

# Create folds
n <- nrow(X)
folds <- sample(rep(1:5, length.out = n))

mu1_hat <- mu0_hat <- pi_hat <- numeric(n)

for (k in 1:5) {
  train_idx <- folds != k
  test_idx <- folds == k
  
  # Propensity score
  fit_pi <- SuperLearner(
    Y = A[train_idx],
    X = X[train_idx, ],
    family = binomial(),
    SL.library = c("SL.glm", "SL.ranger", "SL.xgboost")
  )
  pi_hat[test_idx] <- predict(fit_pi, X[test_idx, ])$pred
  
  # Outcome regression for treated
  fit_mu1 <- SuperLearner(
    Y = Y[train_idx & A[train_idx] == 1],
    X = X[train_idx & A[train_idx] == 1, ],
    SL.library = c("SL.glm", "SL.ranger", "SL.xgboost")
  )
  mu1_hat[test_idx] <- predict(fit_mu1, X[test_idx, ])$pred
  
  # Outcome regression for control
  fit_mu0 <- SuperLearner(
    Y = Y[train_idx & A[train_idx] == 0],
    X = X[train_idx & A[train_idx] == 0, ],
    SL.library = c("SL.glm", "SL.ranger", "SL.xgboost")
  )
  mu0_hat[test_idx] <- predict(fit_mu0, X[test_idx, ])$pred
}

# Trim propensity scores
pi_hat <- pmax(pmin(pi_hat, 0.95), 0.05)

# 3. Compute HOIF estimators
results <- hoif_ate(
  X = X,
  A = A,
  Y = Y,
  mu1 = mu1_hat,
  mu0 = mu0_hat,
  pi = pi_hat,
  transform_method = "splines",
  basis_dim = 5,
  inverse_method = "nlshrink",
  m = 5,
  sample_split = TRUE,
  n_folds = 5,
  seed = 123
)

# 4. Examine results
print(results)
plot(results)

# 5. Extract final estimate
final_ate <- tail(results$ATE, 1)
cat("Final ATE estimate:", round(final_ate, 4), "\n")

Troubleshooting

Python Backend Issues

If you encounter errors with the Python backend:

# Switch to pure R implementation
results <- hoif_ate(
  X = X, A = A, Y = Y,
  mu1 = mu1_hat, mu0 = mu0_hat, pi = pi_hat,
  pure_R_code = TRUE,
  m = 6  # Limited to order 6
)

Numerical Instability

If you see warnings about matrix inversion:

# Try shrinkage methods
results <- hoif_ate(
  X = X, A = A, Y = Y,
  mu1 = mu1_hat, mu0 = mu0_hat, pi = pi_hat,
  inverse_method = "nlshrink"  # or "corpcor"
)

Extreme Propensity Scores

Always trim propensity scores to avoid numerical issues:

# Trim to [0.05, 0.95]
pi_hat <- pmax(pmin(pi_hat, 0.95), 0.05)

References

1. Robins, J. M., Li, L., Tchetgen, E. T., & van der Vaart, A. (2008). Higher order influence functions and minimax estimation of nonlinear functionals. Probability and Statistics: Essays in Honor of David A. Freedman, 335-421.

2. Robins, J. M., Li, L., Mukherjee, R., Tchetgen Tchetgen, E., & van der Vaart, A. (2017). Minimax estimation of a functional on a structured high-dimensional model. Annals of Statistics, 45(5), 1951-1987.

3. Liu, L., Mukherjee, R., & Robins, J. M. (2017). Semiparametric regression in the presence of control variables. Electronic Journal of Statistics, 11(2), 3612-3682.

4. Liu, L., & Li, L. (2023). Stable higher order influence function estimation. arXiv preprint.

Session Info

sessionInfo()
#> R version 4.5.2 (2025-10-31 ucrt)
#> Platform: x86_64-w64-mingw32/x64
#> Running under: Windows 11 x64 (build 26200)
#> 
#> Matrix products: default
#>   LAPACK version 3.12.1
#> 
#> locale:
#> [1] LC_COLLATE=Chinese (Simplified)_China.utf8 
#> [2] LC_CTYPE=Chinese (Simplified)_China.utf8   
#> [3] LC_MONETARY=Chinese (Simplified)_China.utf8
#> [4] LC_NUMERIC=C                               
#> [5] LC_TIME=Chinese (Simplified)_China.utf8    
#> 
#> time zone: Asia/Shanghai
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] HOIF_0.1.0
#> 
#> loaded via a namespace (and not attached):
#>  [1] cli_3.6.5         knitr_1.51        rlang_1.1.7       xfun_0.56        
#>  [5] otel_0.2.0        png_0.1-8         textshaping_1.0.4 jsonlite_2.0.0   
#>  [9] SMUT_1.1          rprojroot_2.1.1   htmltools_0.5.9   ragg_1.5.0       
#> [13] sass_0.4.10       rmarkdown_2.30    grid_4.5.2        evaluate_1.0.5   
#> [17] jquerylib_0.1.4   MASS_7.3-65       fastmap_1.2.0     yaml_2.3.12      
#> [21] lifecycle_1.0.5   compiler_4.5.2    RSpectra_0.16-2   fs_1.6.6         
#> [25] htmlwidgets_1.6.4 Rcpp_1.1.1        here_1.0.2        rstudioapi_0.18.0
#> [29] lattice_0.22-7    systemfonts_1.3.1 digest_0.6.39     R6_2.6.1         
#> [33] reticulate_1.44.1 ustats_0.1.0      Matrix_1.7-4      bslib_0.9.0      
#> [37] withr_3.0.2       SPAtest_3.1.2     SKAT_2.2.5        tools_4.5.2      
#> [41] pkgdown_2.2.0     cachem_1.1.0      desc_1.4.3